Information-Theoretic Principles in the Evolution of Semantic Systems
Abstract
Across the world, languages enable their speakers to communicate effectively using relatively small lexicons compared to the complexity of the environment. How do word meanings facilitate this ability across languages? The forces that govern how languages assign meanings to words, i.e., human semantic systems, have been debated for decades. Recently, it has been suggested that languages are adapted for efficient communication. However, a major question has been left largely unaddressed: how does pressure for efficiency relate to the evolution of semantic systems? This thesis addresses this question by identifying fundamental information-theoretic principles that may underlie semantic systems and their evolution. The main results and contributions of this thesis are structured in three parts, as detailed below.
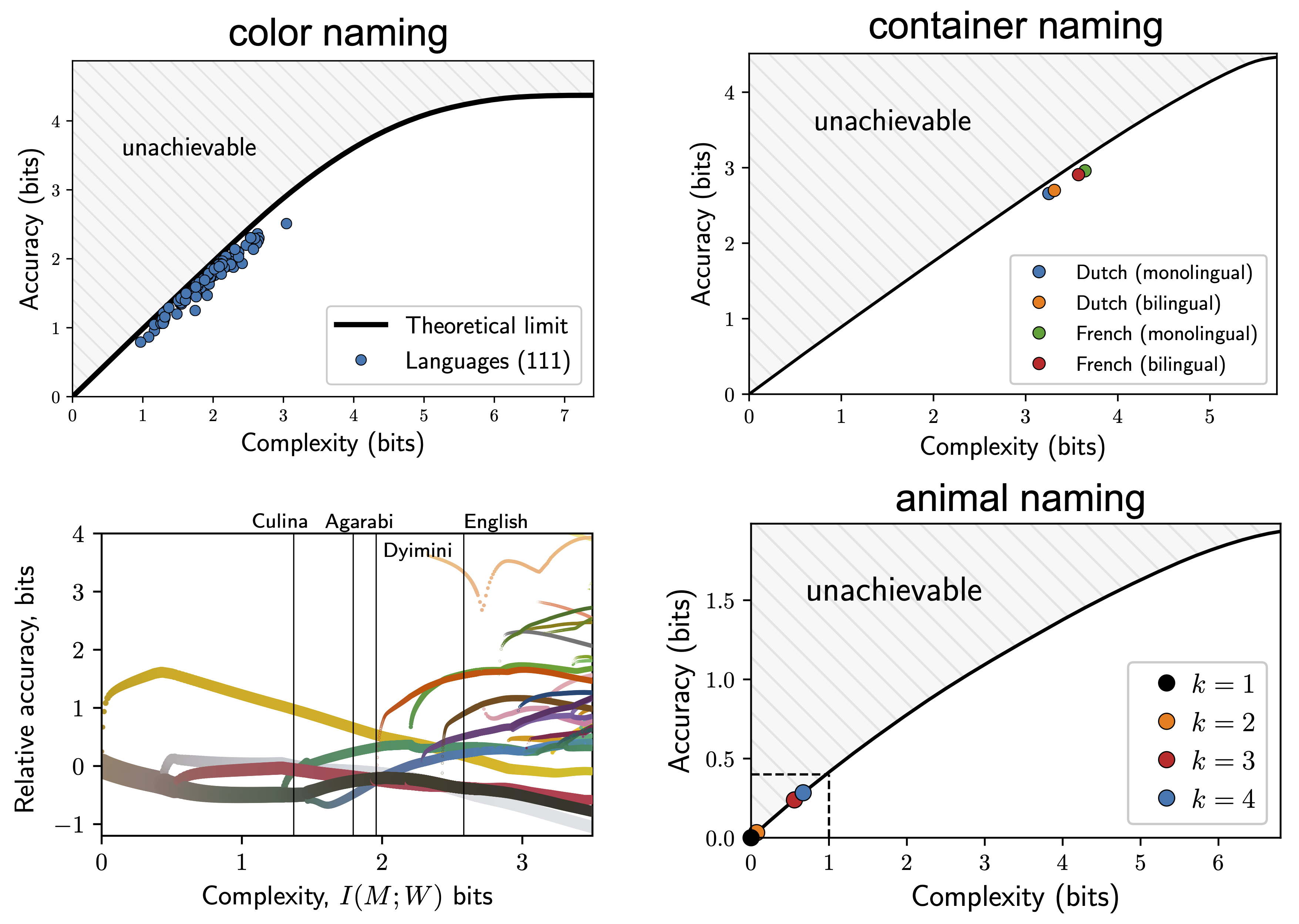
Part I presents our information-theoretic approach to semantic systems and demonstrates its predictive power and empirical advantages. We argue that languages efficiently encode meanings into words by optimizing the Information Bottleneck (IB) tradeoff between the complexity and accuracy of the lexicon. We begin by testing this hypothesis in the domain of color naming, and show that color naming across languages is near-optimally efficient in the IB sense. Furthermore, this finding suggests (1) a theoretical explanation for why empirically observed patterns of inconsistent naming and stochastic categories, which introduce ambiguity, are efficient for communication; and (2) that languages may evolve under pressure for efficient coding through an annealing-like process that synthesizes continuous and discrete aspects of previous accounts of color category evolution. This process generates quantitative predictions for how color naming systems may change over time. These predictions are directly supported by an analysis of recent data documenting changes over time in the color naming system of a single language. In addition, we show that this general approach also applies to two qualitatively different semantic domains: names for household containers, and for animal categories. Taken together, these findings suggest that pressure for efficient coding under limited resources, as defined by IB, may shape semantic systems across languages and across domains.
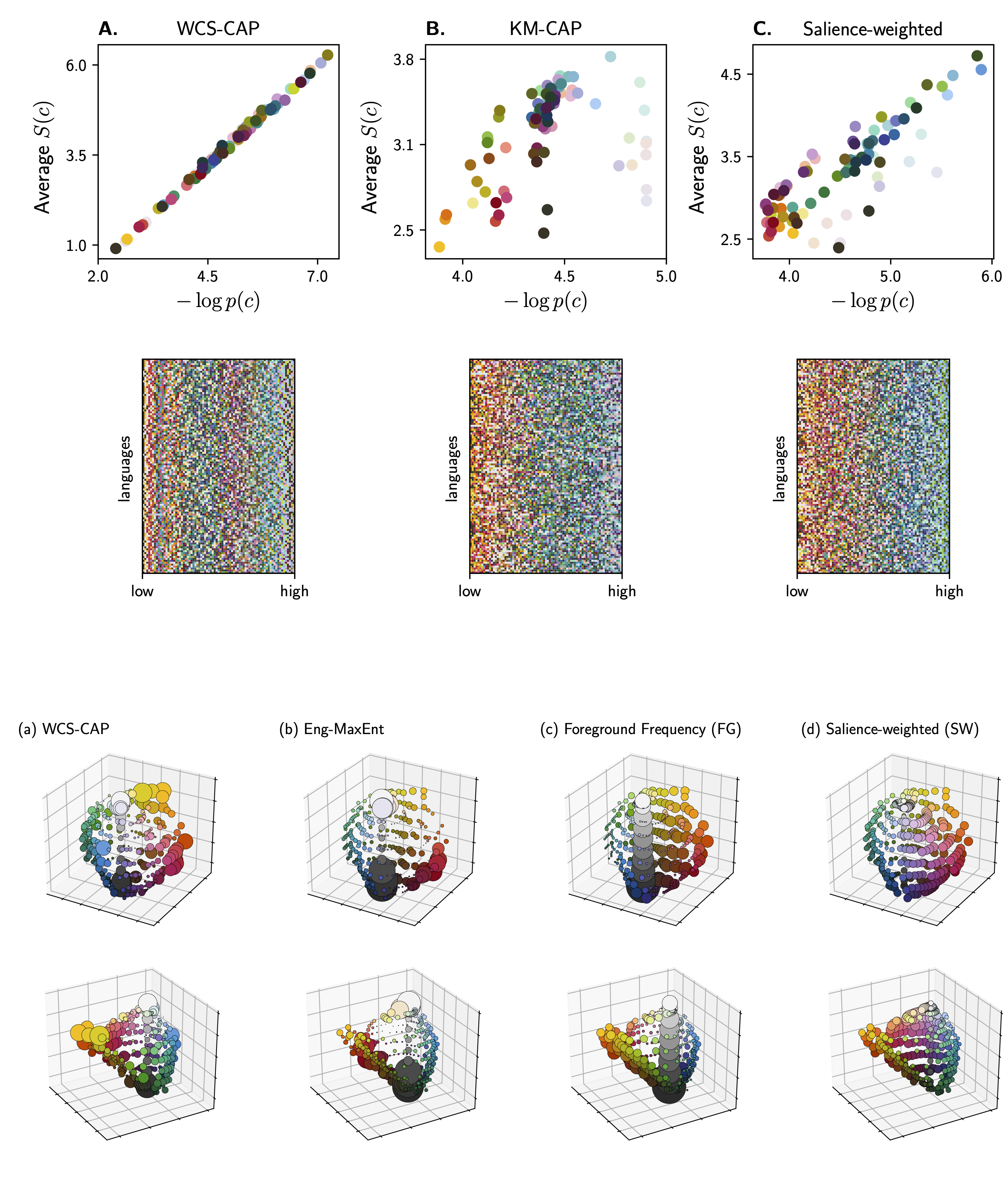
Part II presents an information-theoretic approach for characterizing communicative need. Communicative need is a central component in many efficiency-based approaches to language, including the IB approach mentioned above. It is formulated as a prior distribution over elements in the environment that reflects the frequency with which they are referred to during communication. There is evidence that this component may have substantial influence on semantic systems, however it has not been clear how to characterize and estimate it. We address this problem by invoking two general information-theoretic principles: the capacity-achieving principle, and the maximum-entropy principle. As before, we test this approach in the domain of color naming. First, an analysis based on the capacity-achieving principle suggests that color naming may be shaped by communicative need in interaction with color perception, as opposed to traditional accounts that focused mainly on perception and recent accounts that focused mainly on need. Second, by invoking the maximum-entropy principle with word-frequency constraints, we show that linguistic usage may be the most relevant factor for characterizing the communicative need of colors, as opposed to the statistics of colors in the visual environment. This approach is domain-general, and so it may also be used to characterize communicative need in other semantic domains.
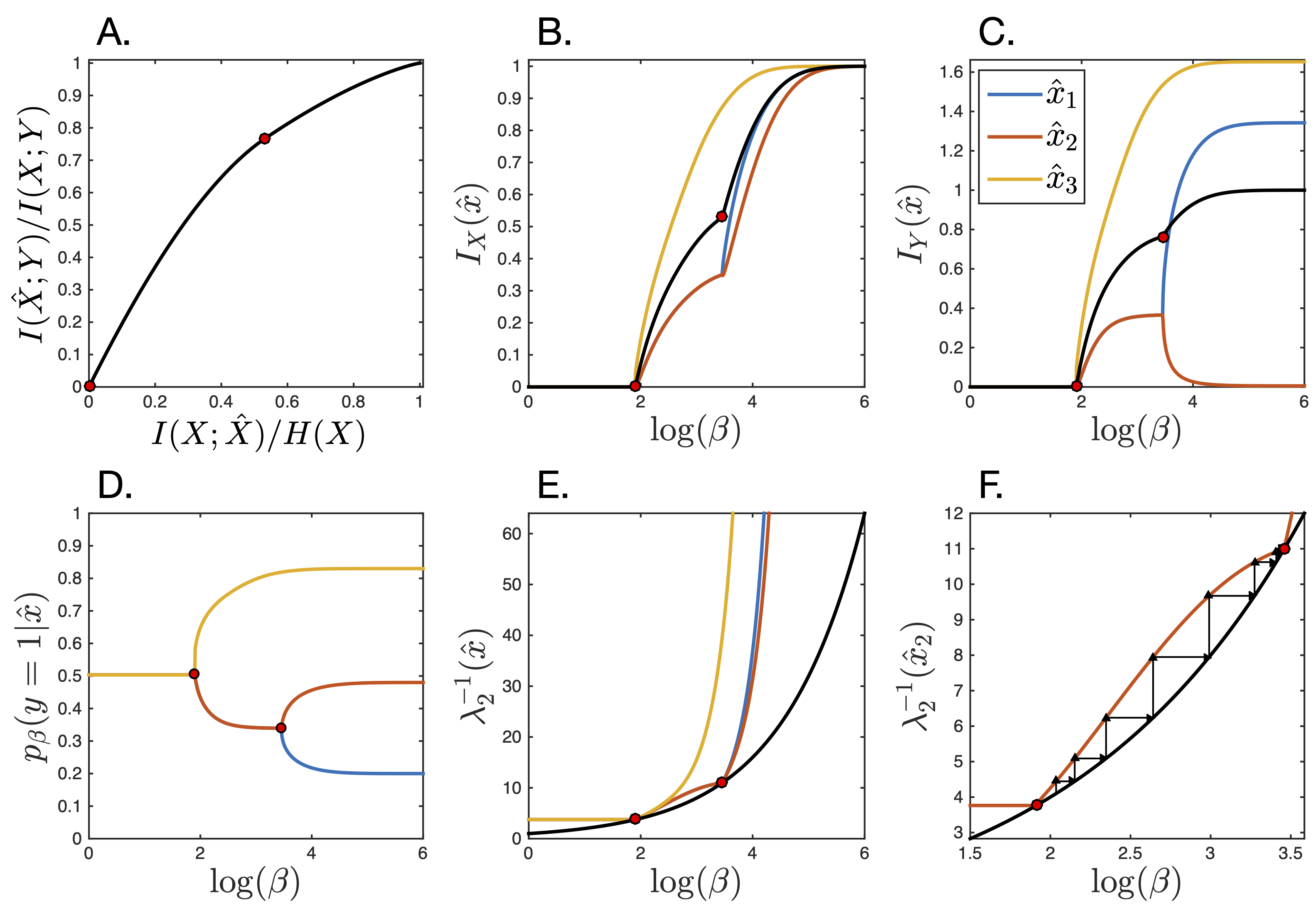
Part III touches on the foundations of the IB framework by extending the mathematical understanding of the structure and evolution of efficient IB representations. This contribution is important given the growing evidence for the applicability of the IB principle not only to language, but also to deep learning, neuroscience, and cognition. Here, we consider specifically the case of discrete, or symbolic, representations, as in our application of IB to the evolution of human semantic systems. We characterize the structural changes in the IB representations as they evolve via a deterministic annealing process; derive an algorithm for finding critical points; and numerically explore the types of bifurcations and related phenomena that occur in IB. These phenomena and the theoretical justification for this approach apply to efficient symbolic representations in both humans and machines. Therefore, we believe that this approach could potentially guide the development of artificial intelligence systems with human-like semantics.
In conclusion, this thesis presents a mathematical approach to semantic systems that is comprehensively grounded in information theory and is supported empirically. Pressure for efficient coding arises as a major force that may shape semantic systems across languages, suggesting that the same principles that govern low-level neural representations may also govern high-level semantic representations.